Fouriertransformationsdarstellung

Im weiteren Verlauf wird die schnelle Fouriertransformation (Fast Fourier Transformation) als FFT abgekürzt. Sämtliche möglichen Darstellungen in diesem Modul fußen auf der Grundlage der FFT der ursprünglichen Zeitreihe. Je nach gewählter Anzahl der Punkte für die FFT wird hier ein mehr oder weniger präzises Bild der Frequenzanteile des Signals dargestellt.

Nehmen wir als Beispiel den Ausschnitt eines tiefen Saxofontons, der aus ca. 135000 Messwerten besteht. Dann wird nach Auswahl des Ausschnitts die maximal mögliche FFT, hier also aus Punkten berechnet und im FFT Fenster dargestellt wie man am Screenshot (Abbildung 4.5) sehen kann.

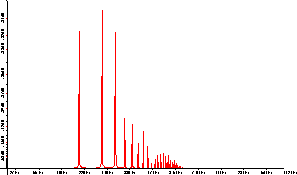
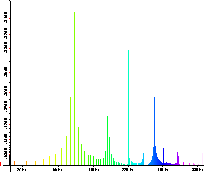
Hier sind die Frequenzen auf der x-Achse mit ihren entsprechenden Amplituden aufgetragen. Die Darstellungsarten lassen sich umstellen, hier handelt es sich um eine doppeltlogarithmische Darstellung.

Ganz oben im FFT-Fenster erkennt man eine Klaviertastatur. Sie dient dem Musiker zur Orientierung, da ein solcher selten mehr als den Kammerton a einer Frequenz zuordnen kann. Außerdem dient sie der Kontrolle der angezeigten Frequenzen, denn wenn man die Klaviatur an irgendeiner Stelle anklickt ertönt der entsprechende Ton aus dem PC-Lautsprecher.

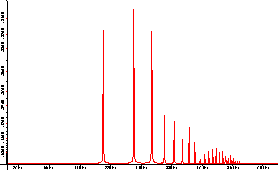
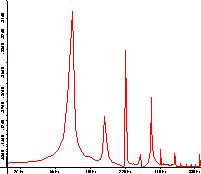
Am linken Rand erkennt man die Amplitudenskala, die die relativen Amplituden der Frequenzanteile bezüglich der Maximalamplitude, die durch die Aufnahmequalität (8bit/16bit) festgelegt ist, angibt. Der Wertebereich sowie die Skalierung, linear oder logarithmisch, sind über die Parameterliste am rechten Rand des Fensters einstellbar. Bei linearer Skalierung sind die Frequenzanteile deutlicher voneinander zu trennen, da die Peaks wesentlich schärfer ausgeprägt sind, jedoch können in dieser Darstellung die höheren Obertöne nicht mehr genügend gut aufgelöst werden. Für die Auswertung empfiehlt sich daher die logarithmische Achseneinteilung. Zum Vergleich dasselbe Spektrum einmal in linearer und logarithmischer Amplitudendarstellung. (Abbildung 4.6 und Abbildung 4.7)

Am unteren Rand des FFT-Moduls ist die Frequenzskala aufgetragen. Der voreingestellte Bereich geht von 20 Hz bis zur halben Samplingrate (also bei einer Aufnahmequalität von 48 kHz bis 24 kHz). Der Grund dafür ist das Shannonsche Abtasttheorem, das besagt, das die höchste durch die FFT detektierte Frequenz kleiner ist als die halbe Abtastfrequenz, denn durch weniger als zwei Punkte kann keine Sinus- oder Kosinusschwingung eindeutig bestimmt werden. Bei einer Abtastrate von 48 kHz wird ja eine ganze 24 kHz Schwingung gerade mal durch zwei Stützstellen erfasst, noch schnellere Schwingungen sind nicht mehr feststellbar. Auch dieser Frequenzbereich kann über die Parameterliste im rechten Bereich des Fensters eingestellt werden, um beispielsweise einen Ausschnitt aus den Frequenzen genauer zu untersuchen. Die Skala ist standardmäßig logarithmisch eingeteilt, was den einfachen Grund hat, dass nur dann Oktaven denselben geometrischen Abstand haben, bzw. die Klaviertastatur so gleichmäßig erscheint wie sie in Wirklichkeit ist. Dazu muss man wissen, dass das Intervall Oktave genau der Verdopplung der unteren Frequenz entspricht, das eingestrichene a hat mit 440 Hz die halbe Frequenz des zweigestrichenen a´s mit 880 Hz.

Nur in der logarithmischen Frequenzeinteilung ist der für Orchesterinstrumente interessierende Bereich gleichmäßig über den Bildschirm verteilt.

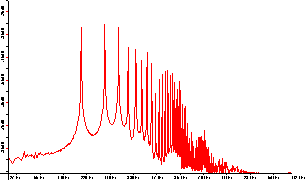
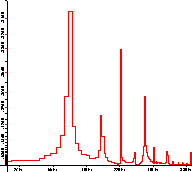
Auch hier in Abbildung 4.8 und Abbildung 4.9 zur Veranschaulichung noch einmal der Vergleich des obigen Saxofontons für beide Achseneinteilungen in einem etwas kleineren Frequenzausschnitt. Der Vorteil an der linearen Darstellung ist aber, dass hier die Obertöne äquidistante Abstände haben, was eine Kontrolle dieser Eigenschaft besonders leicht macht.

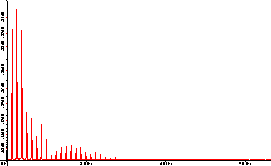
Für die Darstellung der Kurve können drei verschiedene Einstellungen gewählt werden: Balken, Linien und Säulen, die sich nur in der Verbindung der einzelnen Messwerte unterscheiden, am einfachsten lässt sich das auch an einer Grafik zeigen:

Die Liniendarstellung verschmiert die einzelnen Messwerte, die Säulendarstellung trennt die Messwerte deutlich, die Balkendarstellung ist ein Kompromiss, der die Frequenzen noch farblich kennzeichnet. Der Vorteil an der Säulendarstellung ist sicherlich, dass man genau weiß, aus wie vielen Datenpunkten sich gerade in den tiefen Frequenzbereichen die FFT zusammensetzt. Für eine gute Frequenzauflösung in den tiefen Frequenzen ist FFT-bedingt eine höhere Anzahl an Punkten zur Auswertung vorzusehen, also die FFT-Größe anzuheben. Hier wird man statt der 4096 Punkte eher 16.384 Punkte nehmen, sofern man genügend lange Töne oder hohe Samplingraten zur Verfügung hat. Wechselt der Ton innerhalb dieser Punkte, so verschmiert auch die FFT.

Zwei weitere Einstellmöglichkeiten stehen unter dem Punkt „Darstellung“ noch zur Verfügung. Setzt man bei „Maxima merken“ einen Haken, so bekommt man eine „addierte“ FFT, denn der Rechner merkt sich dann von allen vorhergehenden FFT Berechnungen für jeden Frequenzkanal die höchste Amplitude und aktualisiert diese nur, wenn bei derselben Frequenz eine nachfolgende FFT eine noch größere Amplitude hat. Auf diese Weise kann man so eine Art zweites Leistungsspektrum generieren. Lässt man mit dieser Funktion ein Instrument seinen ganzen Tonumfang durchspielen, so kann man an dieser „Summen- FFT“ ablesen, in welchen Frequenzbereichen am wenigsten Amplitude abgestrahlt wird, oder ob die Abstrahlung über den gesamten Tonumfang gleichmäßig ist. Man kann das vielleicht mit einem Absorptionsspektrum aus der Astronomie vergleichen, nur das der Filter hier nicht Atmosphären sind, sondern Eigenresonanzen der Instrumente.

Die zweite Einstellmöglichkeit heißt „Delay“ und macht nichts anderes als bei kontinuierlicher FFT Berechnung, wie sie beim Abspielen von Dateien durchgeführt wird, ein etwas fließenderes Bild zu liefern, eine sogenannte Wasserfalldarstellung deren Tempo man einstellen kann. Der Rechner merkt sich die alte FFT und für jede neue Iteration werden die alten Werte ein wenig abgeschwächt. Die Frequenzen bei denen die neue FFT die alten Amplitudenwerte übertrifft, werden auf die neuen Werte heraufgesetzt. So erhält man fließende Übergänge zwischen den FFTs. Der Effekt lässt sich leider nicht durch Bilder illustrieren, sondern nur am Rechner sichtbar machen.

In der Regel interessiert man sich für die Peaks der FFT, d.h. versucht aus dem Amplitudenverlauf die Frequenzen abzuleiten, die in dem Klang enthalten sind. Jede FFT liefert ja transformationsbedingt eine gewisse Unschärfe, selbst wenn der analysierte Ton ein reiner Sinuston ist. Die Ursache liegt darin, dass für die Analyse ja nur ein Ausschnitt aus dem Ton verwendet wird, und nicht die unendliche Sinusschwingung. Gibt es aber ein Anfang und ein Ende der Sinusschwingung, so findet die Analyse an diesen Rändern einen Bruch vor, den sie in viele eng an der Ursprungsfrequenz liegende Frequenzen zerlegt. Dabei gilt, je mehr Punkte einer festen Schwingung zur Verfügung stehen, desto präziser wird auch die FFT. Nun gibt es viele Verfahren die Peaks aus einer solchen FFT herauszufiltern und es wurde versucht diese nachzuempfinden und zu programmieren. Man kann z.B. die Steigung in jedem Punkt berechnen und davon ausgehen, dass man dann einen Peak gefunden hat, wenn die Steigung jäh das Vorzeichen wechselt. Nur gibt es bei den FFTs mit tausenden von Messpunkten auch statistisch bedingte Zwischenpeaks, die bei Betrachtung mit dem Auge sofort als unwichtig eingestuft würden, die aber ein Algorithmus nur durch weitere Bedingungen herausfiltern kann. Als Zusatz wurde die Bedingung programmiert, das zwischen zwei Peaks mindestens eine bestimmte einstellbare Anzahl von Messwerten liegen muss, in denen kein Peak vorkommt, was für monophone Aufnahmen sicher ein ganz guter Filter ist, für polyphone Stücke aber versagen muss. Auch muss der Peak eine bestimmte Amplitude haben, damit er als Peak anerkannt wird. Hierunter leiden aber vor allem die hochfrequenten Obertöne, die prinzipiell geringere Amplituden haben, da sie ja nur mitschwingen.

In der Parameterleiste des FFT-Moduls kann man die Peakermittlung aktivieren und an den Parametern „minimaler Abstand zwischen zwei Maxima“ und „minimaler Abstand vom Peak ab dem die Amplitude auf 20% der Peakamplitude abgesunken ist“ solange drehen, bis die mit dem Auge relativ schnell auffindbaren Peaks auch vom Rechner zufriedenstellend gefunden werden.

In einer weiteren Rubrik der Parameterleiste können dann die so gefundenen Peaks durch drei verschiedene Splinealgorithmen miteinander verbunden werden, wobei sich der B- Spline als der treffendste erweist. Hintergrund dieser Optimierungsdarstellung ist der Wunsch Formanten, also einfach gesagt: die Stärken und Schwächen im Obertonspektrum, darzustellen.

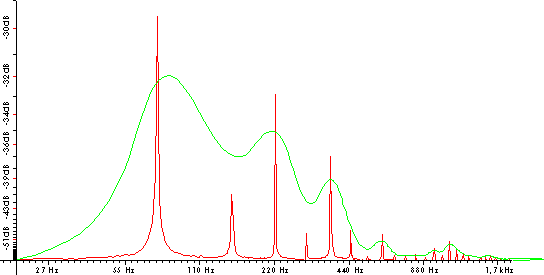
In der Abbildung 4.13 ist so eine Optimierungskurve gezeichnet, die deutlich macht, dass bei diesem Kontrabasston die jeweils ungeradzahligen Obertöne deutlich schwächer sind als der Grundton und die geradzahligen Obertöne. Ist die Funktion „Peaks ermitteln“ aktiviert, so kann außerdem die Form der Splinekurve mit Hand nachkorrigiert werden, indem man genau wie bei der Optimierung der Hüllkurve Stützpunkte durch Anklicken mit der rechten Maustaste entweder hinzufügt oder entfernt.

In diesem Modul gibt es noch zwei weitere Funktionen, die kurz erläutert werden. So gibt es die Möglichkeit, jederzeit, auch während der laufenden Wiedergabe oder Aufnahme, über die linke Maustaste die dortige Frequenz auf 5 Stellen genau ausgeben zu lassen. Wird die Maustaste gedrückt gehalten, so erscheint eine senkrechte weiße Linie mit einer Frequenzangabe, die den genauen Frequenzwert an dieser Stelle ausgibt. Auf diese Weise kann man einzelne Peaks im Spektrum genau vermessen. Die zweite Funktion betrifft die für die aktuelle Darstellung verwendete FFT- Größe, die permanent in einem Infobereich der Parameterleiste zusätzlich angezeigt wird.

Wie man sehen kann, ist die reine Darstellung der Ergebnisse einer FFT schon sehr informationsträchtig und bietet sich für erste wichtige Analysen an. Viele weitere Funktionen des Programms bauen darauf auf, wie der nächste Abschnitt zeigt.