Home » Zeitreihenanalyse <Seite zurück

Zeitreihenanalysefenster

In diesem Modul sind die folgenden Analysemethoden implementiert: Maximaler Lyapunovexponent, Lyapunovexponentenspektrum sowie Korrelationsdimensionsbestimmung. Über Auswahlbuttons können die entsprechenden Berechnungsverfahren aufgerufen werden. Der Screenshot (Abbildung 4.23) zeigt die Berechnung des Lyapunovexponentenspektrums vom Lorenzattraktor. Je nachdem welches Verfahren man ausgewählt hat, sind die Einstellungen im Parameterbereich leicht unterschiedlich. Die verschiedenen Algorithmen benötigen unterschiedliche Argumente, die hier angepasst werden können. Allen gemeinsam ist die Wahl des Zeitverzögerungsparameters „Tau“ und der Wahl der von der ausgewählten Zeitreihe für die Berechnungen verwendeten Punkte.
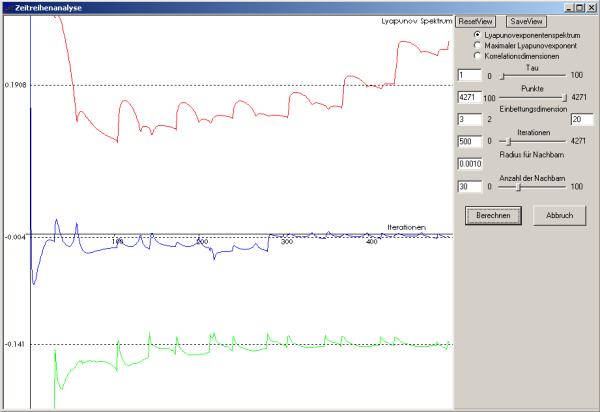
Lyapunovspektrum Aufgetragen sind die Werte der verschiedenen Lyapunovexponenten (für jede Einbettungsdimension einer) über der Zahl der Iterationen der Berechnung. Beide können als Parameter eingestellt werden. Die maximale Anzahl an Iterationen ist dabei durch die Anzahl der verwendeten Punkte gegeben. Je mehr Iterationen angegeben werden, desto länger ist die Rechenzeit, aber desto genauer wird die Bestimmung der Exponenten. Der Parameter „Radius für Nachbarn“ ist die prozentuale Angabe des Radius der Umgebung in der Nachbarn gesucht werden sollen, mit der die Iterationen gestartet werden. Der Algorithmus passt diesen Startwert im Laufe der Rechnungen selber an. Der Parameter „Anzahl der Nachbarn“ passt die Zahl der nächsten Nachbarn an, die in die Auswertung gelangen. Werden vom Algorithmus mehr Nachbarn gezählt, wird nur die hier spezifizierte Anzahl verwendet. Nach Fertigstellung der Berechnung geben die gestrichelten Linien die ermittelten Exponenten an, deren Werte links an der Skala abgelesen werden können. Die Auswertung erfolgt dann mit Hilfe von Vergleichen. Bei unserem Beispiel handelt es sich nach dieser Analysemethode offensichtlich um einen chaotischen Attraktor, da das Spektrum der Exponenten in der Kombination (+, 0, -) also positiv, nahe null und negativ auftaucht, was nur ein Merkmal dieser Art von Attraktoren ist.
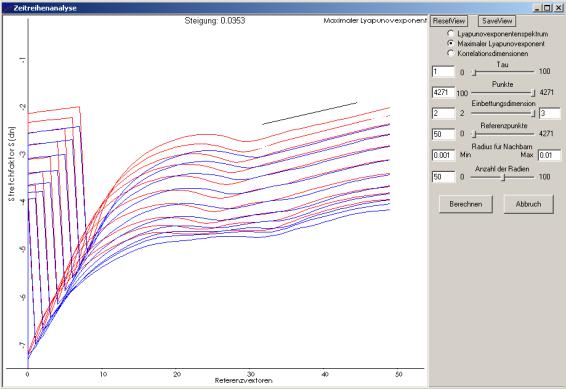
Maximaler Lyapunovexponent Auf dem Screenshot (Abbildung 4.24) sieht man die Berechnung des maximalen Lyapunovexponenten für dieselbe Zeitreihe wie eben. Hier kann man für die Einbettungsdimension einen Bereich angeben, wenn der Exponent aus den Daten in verschiedenen Dimensionen berechnet werden soll, bzw. um zu prüfen, ob die richtige Einbettungsdimension gewählt wurde. Im Parameterbereich kann noch die Anzahl der „Referenzpunkte“ reduziert werden, also von wie vielen zufällig ausgewählten Punkten die Ermittlung des exponentiellen Auseinanderlaufens vorgenommen werden soll. Werden hier alle verfügbaren gewählt, wie es die Theorie vorschreibt, so gerät man schnell an die Leistungsgrenzen jedes Rechners und ist gut beraten diese Zahl zu reduzieren. Die Ergebnisse erfordern dann aber eine sorgfältigere Prüfung und Bewertung. Mit dem minimalen und maximalen Radius für Nachbarn wird der prozentuale Bereich angegeben, in dem Nachbarn von denen aus benachbarte Trajektorien starten können, gesucht werden. Diese Zone wird für die Berechnungen in die unter „Anzahl der Radien“ festgelegte Anzahl von Schritten unterteilt, so dass dann entsprechend viele Messkurven multipliziert mit der Anzahl der Einbettungsdimensionen vorliegen. In der Auswertegrafik ist der Stretchfaktor über den Referenzvektoren aufgetragen und die Graphen für unterschiedliche Einbettungsdimensionen farblich codiert. Gibt es nach der Berechnung Bereiche der Kurvenschar, in denen die Hauptzahl der Graphen eine lineare Zone hat, dann kann davon ausgegangen werden, dass hier ein exponentielles Auseinanderdriften der Trajektorien stattgefunden hat, da der Stretchfaktor ein logarithmisches Maß ist. Die Steigung in diesem Bereich gibt den maximalen Lyapunovexponenten an und wird ermittelt, in dem man mit der Maus eine Steigungsgerade aufzieht, deren Steigung dann im oberen Mittelteil des Fensters ausgegeben wird. In unserem Beispiel sieht man die gezeichnete Steigungslinie leicht oberhalb der Graphen in schwarz und der berechnete Steigungswert ist der maximale Lyapunovexponent von 0,0353.
Ein wichtiger Hinweis betrifft die Aussagekraft dieser Darstellung. Nicht jeder Zeitreihe kann ein maximaler Lyapunovexponent zugeordnet werden. Gerade bei den musikalischen Zeitreihen gibt es in den Graphen oft keinen linearen Bereich, d.h. die Trajektorien laufen nicht exponentiell auseinander, was sich mit der früheren Erkenntnis aus dem Rekonstruktionsmodul deckt. Durch die Art der Darstellung des Stretchfaktors über den Referenzvektoren kann festgestellt werden, ob die Aussage eines maximalen Lyapunovexponenten überhaupt sinnvoll oder eine Aussage nicht möglich ist. Daher wurde der vielleicht auf den ersten Blick etwas umständliche Weg der Steigungsbestimmung „per Hand“ gewählt.
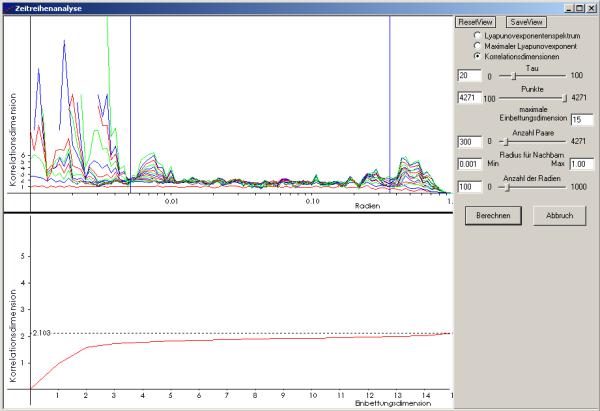
Korrelationsdimension Für dieselbe Zeitreihe des Lorenzattraktors wird nun auch die Korrelationsdimension berechnet. In der Abbildung 4.25 sieht man, dass dieses Fenster ist in zwei Abschnitte unterteilt ist. Im oberen befinden sich die eigentlichen Berechnungen, im unteren sieht man eine Zusammenstellung der Ergebnisse. Bei diesem Verfahren wird ja die Anzahl der Nachbarn in verschiedenen Hyperkugeln um die Referenzpunkte ermittelt und über alle Referenzpunkte gemittelt. Diese Mittelwerte sind also abhängig von der Einbettungsdimension und dem gewählten Radius der Hyperkugeln. Im oberen Teil des Fensters wird daher die ermittelte Korrelationsdimension über dem verwendeten Radius in Abhängigkeit der farblich codierten Einbettungsdimension aufgetragen. Im unteren Bereich werden dann für jede Einbettungsdimension die Korrelationssummen über alle Radien gemittelt und diese Mittelwerte über den Einbettungsdimensionen aufgetragen. In aller Regel konvergiert die Kurve asymptotisch gegen die Korrelationsdimension. Damit man aber auch hier keine unsinnigen Bereiche auswertet, muss man im oberen Fenster durch drücken der linken Maustaste einen Bereich zur Auswertung angeben, der durch zwei senkrechte blaue Linien gekennzeichnet wird. Für zu kleine oder zu große Radien wird die Korrelationsdimension nämlich fehlerhaft. Der relevante Bereich zeichnet sich als Plateau über alle Dimensionen ab. Im Parameterbereich kann die maximale Einbettungsdimension angegeben werden, bis zu Die einstellbare „Anzahl der Paare“ ist ein Wert der dem Algorithmus vorschreibt, dass er bei der Berechung der Nachbarn höchstens für diese Anzahl an Punktepaaren die Abstände berechnet. Der Wert dient der Temposteigerung, sollte aber nicht zu niedrig liegen. Ein Wert von 1000 hat sich bewährt. Die minimale und maximale Radiusangabe bzw. die entsprechende „Anzahl der Radien“ dazu beschreibt in welchem Bereich der Algorithmus die Hyperkugeln bilden soll um nach Nachbarn zu suchen und mit wie vielen Unterstufen. Hierbei gilt, je präziser die Differenzierung und je weiter der Bereich, desto treffsicherer die Auswertung. Die vom Programm vorgesehenen Standardvorgaben sind aber ein guter Anfang. Bei allen drei Zeitreihenanalyseverfahren hat man die Möglichkeit bei falscher Wahl der Parameter die Berechnung mit ESC oder dem Button „Abbruch“ während der Bearbeitung zu beenden, da man sich in der Rechenzeit oft verschätzt. Der Abbruchvorgang kann aber unter Umständen auch kurze Zeit dauern, die durch das Aussehen des Cursors als Sanduhr angezeigt wird.